Der Physik Nobelpreis 2024 ging an John J. Hopfield und Geoffrey Hinton „für bahnbrechende Entdeckungen und Erfindungen, die maschinelles Lernen mit künstlichen neuronalen Netzen ermöglichen“.
Die Bilder und mathematischen Erläuterungen dieses Artikels sind dem Video A Brain-Inspired Algorithm For Memory entnommen, oder orientieren sich an der Presseerklärung des Nobelpreiskomitees.
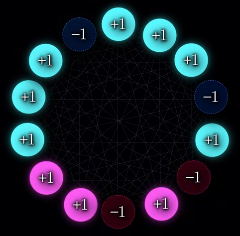
John Hopfield erfand 1982 ein Netzwerk, das eine Methode zum Speichern und Wiederherstellen von Mustern liefert. Wir können uns die Knoten des Netzwerks z.B. als Pixel eines Bildes vorstellen, wobei +1 einen schwarzen Pixel und -1 einen weißen Pixel repräsentiert.
Eine bestimmte Konfiguration in diesem Netzwerk wird durch eine Energie beschrieben, die der eines Systems winziger Magneten entspricht. In der Physik spricht man von Ising Spin Modellen. Das Hopfield Netz wird so trainiert, dass Werte für die Verbindungen zwischen den Knoten gefunden werden, die zu minimaler Energie führen. Es gilt:
$$ E= -\sum_{ij} w_{ij} x_i x_j $$
Für Verbindungen zwischen Knoten mit gleichem Vorzeichen muss \(\omega_{ij}\) also > 0 sein und für Verbindungen mit ungleichem Vorzeichen < 0 um die Energie zu minimieren.
Wenn das trainierte Hopfield-Netzwerk mit einem verzerrten oder unvollständigen Bild gefüttert wird, arbeitet es sich methodisch durch alle Knoten und aktualisiert die Werte, sodass die Energie des Netzwerks sinkt. Dazu berechnen wir zunächst für den zu verändernden Knoten \(i\) die gewichtete Summe h über alle Nachbarknoten. Ist \(h_i > 0\) , wird der Knoten auf +1 gesetzt und für \(h_i\ < 0\) auf -1.
$$ h_i = w_{i1}x_1 + \cdots + w_{iN}x_N = \sum_{j \neq i} w_{ij} x_j $$
Das Netzwerk arbeitet schrittweise, um das gespeicherte Bild zu finden, das dem unvollkommenen Bild, am ähnlichsten ist.
Doch wie sollen die Gewichtungen \(\omega\) gesetzt werden? Soll nur eine einzige Konfiguration \(\zeta\) gespeichert bzw. angelernt werden, gilt ein einfachster Ansatz \(\omega_{ij} = \zeta_i\zeta_j\) . Sollen mehrere sehr unterschiedliche Konfigurationen \(\zeta\) trainiert werden gilt \(\omega_{ij} = \zeta^1_{ij}+\zeta^2_{ij}+...\)
Veranschaulicht man sich dies im Konfigurationsraum wird deutlich, dass die Konfigurationen für diesen Ansatz 'weit' voneinander 'entfernt' sein müssen. Der von Hopfield gewählte Ansatz ist daher noch wenig von praktischem Nutzen, da die maximale Zahl der speicherbaren Muster nur ca. 0.14 mal der Zahl der Knoten oder Neuronen entspricht.
Geoffrey Hinton nutzte das Hopfield-Netzwerk als Grundlage für ein neues Netzwerk, das eine andere Methode verwendet: die Boltzmann-Maschine. Die Boltzmann Maschine kann charakteristische Elemente in den Daten erkennen. Der neue Ansatz besteht darin dem Netzwerk neben den 'sichtbaren' Neuronen sogenannte 'unsichtbare' Neuronen hinzuzufügen. Diese sind im Bild unten violett gefärbt.
Alle Neuronen sind über eine Matrix \(\omega_{ij}\) miteinander gekoppelt. Die Maschine wird trainiert, indem man die sichtbareren Neutronen mit Beispielen füttert, die mit hoher Wahrscheinlichkeit auftreten. Sowohl sichtbare als auch unsichtbare Neuronen werden jedoch neu gesetzt wenn die Maschine läuft. In der statistischen Physik beschreibt die Boltzmann-Verteilung die Wahrscheinlichkeit, dass ein System in einem bestimmten Zustand \(S_E\) mit der Gesamtenergie \(E\) bei einer Temperatur \(T\) ist. Die Formel lautet:
$$p(S_E) = \frac{1}{Z} e^{-E/T} \, \text{;} \quad Z = \sum_{S_j} e^{-E_j/T}$$
Hierbei bezeichnet \(Z\) die Zustandssumme, die alle möglichen Zustände des Systems berücksichtigt.
Für die Wahrscheinlichkeit eines aktivierten Zustand \(S_{on}\) mit \(E_{on}=E-E_{off}\) gilt daher:
$$p_{on}= \frac{1}{Z} e^{-E_{on}/T} = \frac{e^{-E_{on}}}{e^{-E_{on}}+e^{-E_{off}}}= \frac{1}{1+e^{\Delta E}}$$
Dies entspricht der häufig in der Statistik und im maschinellen Lernen verwendeten Sigmoid Aktivierungsfunktion.
Definieren wir die Energie des Systems ähnlich wie in Hopfield Netzwerken durch
$$ E= -\sum_{ij} w_{ij} x_i x_j $$
so stellt sich erneut die Frage, wie \(\omega_{ij}\) während des Trainingsvorgangs gesetzt bzw. aktualisiert werden soll. Dazu betrachten wir zunächst den Logarithmus der Wahrscheinlichkeit \(P(S)\) eines Datensatzes \(S\) mit Einzeldatensätzen \(x^{(n)}\). Es gilt:
\begin{eqnarray}\log P(\text{S}) & = & \log \left[ \prod_{n=1}^{N} P(x^{(n)}) \right]= \sum_{n=1}^{N} \log P(x^{(n)}) \\ & = & \sum_{n=1}^{N} \log \left( \frac{1}{Z} e^{-E(x^{(n)})/T} \right) \\ & = & \sum_{n=1}^{N} \left( \frac{-E(x^{(n)})}{T} - \log Z \right) \\ & = & -\frac{1}{T} \sum_{n=1}^{N} E(x^{(n)}) - N \log Z\end{eqnarray}
Die Schritte \(\Delta\omega_{ij}\) mit denen sich \(\omega_{ij}\) während des Trainings ändern soll, seien wie folgt definiert:
\[\Delta\omega_{ij} = \frac{\partial \log P(\text{S})}{\partial w_{ij}} = \frac{1}{T} \sum_{n=1}^{N} \frac{\partial E(x^{(n)})}{\partial w_{ij}} - N \frac{\partial \log Z}{\partial w_{ij}}\]
Dadurch ist gewährleistet dass sich \(\omega_{ij}\) bei Erreichen von hoher Wahrscheinlichkeit bzw niedriger Gesamtenergie nicht mehr ändert.
Der erste Term lässt sich zu
\[\frac{\partial}{\partial w_{ij}} E(x^{(n)}) = \frac{\partial}{\partial w_{ij}} \left[ - \sum_{ij} w_{ij} x_i x_j \right] = - x_i x_j\]
vereinfachen, und für den zweiten Term gilt:
\begin{eqnarray}\frac{\partial}{\partial w_{ij}} \log Z & = &\frac{1}{Z} \frac{\partial}{\partial w_{ij}} \left[ \sum_{s} e^{-E(s)} \right]= \frac{1}{Z} \sum_{s} \left[ e^{-E(s)} \frac{\partial}{\partial w_{ij}} [-E(s)] \right] \\ & = & \frac{1}{Z} \sum_{s} e^{-E(s)} x_i^s x_j^s = \sum_{s} \frac{e^{-E(s)}}{Z} x_i^s x_j^s = \sum_{s} p(s) x_i^s x_j^s\end{eqnarray}
Ingesamt gilt also:
\[\Delta\omega_{ij}=\frac{\partial \log P(\text{data})}{\partial w_{ij}} = \frac{1}{T} \left( \sum_{n=1}^{N} (x_i x_j)_{\text{data}} - N \sum_{s} p(s) x_i^s x_j^s \right)\]
oder prägnanter:
\[\Delta\omega_{ij} \propto \, \langle x_i x_j \rangle_N - \langle p(s)x_i x_j \rangle_S\]
Dabei bezeichnet der erste Term, der auch Hebbian Term genannt wird, den Mittelwert eines Neuronenpaares \(x_i x_j\) über alle \(N\) Neuronen des Trainingsdatensatzes, und der zweite Term, der Anti Hebbian Term genannt wird, den Mittelwert über alle Zustände die mit der Wahrscheinlichkeit \(p(s)\) eingenommen werden. Während des Trainings der Boltzmann Maschine wird die Kopplung zwischen den Neuronen also so lange verändert, bis der Gleichgewichtszustand, der sich idealerweise ergibt wenn die Boltzmann Maschine läuft und die Neuronen ändert, nicht mehr vom Trainingsdatensatz unterscheidet.
Auf Grund der Tatsache, dass beim Training und Betrieb einer klassischen Boltzmann Maschine alle Neuronen einzeln durchlaufen werden müssen, sind klassische Boltzmann Maschinen recht langsam. Die sogenannte 'Restricted Boltzmann Machine' (RBM) schafft hier Abhilfe.
Bei der RBM bestehen keine Verbindungen zwischen den einzelnen sichtbaren und den einzelnen unsichtbaren Neuronen mehr. Das Netzwerk zerfällt in 2 Schichten. Dadurch können die sichtbaren und unsichtbaren Neuronen jeweils als Vektor betrachtet werden und in einem Rechenschritt aktualisiert werden.
Hinton hat in seinem Aufsatz 'A Practical Guide to Training Restricted Boltzmann
Machines' die Energie eines solchen Systems durch
$$E(\mathbf{v}, \mathbf{h}) = - \sum_{i \in \text{visible}} a_i v_i - \sum_{j \in \text{hidden}} b_j h_j - \sum_{i,j} v_i h_j w_{ij}$$
beschrieben.
Der Ausdruck deckt sich im Wesentlichen mit dem für klassische Boltzmann Maschinen, wird aber durch Variablen \(a\) für sichtbare und \(b\) für unsichtbare Neuronen in entsprechenden Zusatztermen ergänzt.
Nach Asja Fischer und Christian Igel sind die Wahrscheinlichkeit p(h) ein verstecktes Neuron zu setzen gegeben durch
$$\begin{align*} p(H_i = 1 \mid \mathbf{v}) &= \text{sig} \left( \sum_{j=1}^{m} w_{ij} v_j + a_i \right) \\ p(V_j = 1 \mid \mathbf{h}) &= \text{sig} \left( \sum_{i=1}^{n} w_{ij} h_i + b_j \right) \end{align*}$$
Auch eine RBM wird durch die sogenannte Contrastive Divergence (CD) trainiert. Wie bereits für klassische Boltzmann Maschinen beschrieben, versucht man den Gradienten der Energiefunktion oder der Wahrscheinlichkeit eines finalen Zustandes zu schätzen. Konkret macht man das bei einer RBM in dem man aus der Datenverteilung und ihrer Umkehrung sampelt. Dies umfasst die folgenden Schritte:
- Positive Phase: Beginne mit einer Datenprobe und berechne die versteckten Aktivierungen.
- Negative Phase: Rekonstruiere die sichtbaren Einheiten aus den versteckten Aktivierungen und berechne dann erneut die versteckten Aktivierungen aus diesen Rekonstruktionen.
- Gewichtsaktualisierung: Passe die Gewichte basierend auf dem Unterschied zwischen der Datenverteilung und der rekonstruierten Verteilung an.
Im Oktober 2006 hat Netflix einen offenen Wettbewerb für den besten kollaborativen Filteralgorithmus zur Vorhersage von Nutzerbewertungen für Filme, basierend auf früheren Bewertungen ausgeschrieben.
Gewonnen hat den ausgeschriebenen Preis letztlich im September 2009 die BellKor Solution unter Verwendung einer Restricted Boltzmann Machine.
Ich habe versucht Ähnliches zu programmieren, und unter Verwendung von gewöhnlichen Python Bibliotheken eine RBM erstellt. Der vollständige Python Code kann auf Kaggle als Notebook ausprobiert werden. Die verwendeten Datensätze wurden über die MovieLens-Website während des siebenmonatigen Zeitraums vom 19. September 1997 bis zum 22. April 1998 gesammelt, und vom GroupLens Research Project an der University of Minnesota zusammengestellt. Insgesamt besteht der Datensatz aus 100.000 Bewertungen (1-5) von 943 Nutzern für 1682 Filme. Jeder Nutzer hat mindestens 20 Filme bewertet. Darüber hinaus sind einfache demografische Informationen der Nutzer (Alter, Geschlecht, Beruf, Postleitzahl) enthalten.
Im ersten Schritt werden die nötigen Bibliotheken, sowie die Trainings- und die Testdatensätze geladen. Dann werden die Datensätze in die gewünschte Form gebracht, und letztlich in einem Torch Tensor abgelegt. Die ursprünglichen Bewertungen der Filme reichen von 0 - 3 Sternen. Wir verwenden der Einfachheit halber nur '-1' für 'not rated' , '0' für 'not liked' und '1' für 'liked'.
# ### Importing the libraries import numpy as np import pandas as pd import torch import torch.nn as nn import torch.nn.parallel import torch.optim as optim import torch.utils.data from torch.autograd import Variable # ### Importing the dataset and preparing the training set and the test set training_set = pd.read_csv('/kaggle/input/movielens-100k-dataset/ml-100k/u1.base', delimiter = '\t') training_set = np.array(training_set, dtype = 'int') # format of training_set is user id | movie id | rating | timestamp test_set = pd.read_csv('/kaggle/input/movielens-100k-dataset/ml-100k/u1.test', delimiter = '\t') test_set = np.array(test_set, dtype = 'int') # ### Getting the number of users and movies nb_users = int(max(max(training_set[:, 0], ), max(test_set[:, 0]))) # Calculate number of users nb_movies = int(max(max(training_set[:, 1], ), max(test_set[:, 1]))) # Calculate number of movies # ### Converting the data into an array with users in lines and movies in columns def convert(data): new_data = [] for id_users in range(1, nb_users + 1): id_movies = data[:, 1] [data[:, 0] == id_users] # Create boolean mask for all lines in 1st column matching user_id and transfer data of 2nd column to id_movies vector id_ratings = data[:, 2] [data[:, 0] == id_users] ratings = np.zeros(nb_movies) ratings[id_movies - 1] = id_ratings new_data.append(list(ratings)) return new_data # The reason why we make a list within a list is that torch wants the data in this structure training_set = convert(training_set) test_set = convert(test_set) # ### Converting the data into Torch tensors training_set = torch.FloatTensor(training_set) test_set = torch.FloatTensor(test_set) # Tensors are simply an multidimensional array containing elements of a single data type. They can be processed in gpu or tpu (Tensor Processing Unit). Tensorflow also has a tensor structure, but Pytorch is easier to implement. # ### Converting the ratings into binary ratings 1 (Liked) or 0 (Not Liked) training_set[training_set == 0] = -1 # not rated training_set[training_set == 1] = 0 # not liked training_set[training_set == 2] = 0 # not liked training_set[training_set >= 3] = 1 # liked test_set[test_set == 0] = -1 test_set[test_set == 1] = 0 test_set[test_set == 2] = 0 test_set[test_set >= 3] = 1
# ### Creating the architecture of the Neural Network class RBM(): def __init__(self, nv, nh): self.W = torch.randn(nh, nv) # Initializing the weight between nodes. Initial weight is according to the normal distribution in dimensions nh and nv. self.a = torch.randn(1, nh) # Initial bias value a for the visable node. 1 row and nh columns. Each element is a random number drawn from a standard normal distribution self.b = torch.randn(1, nv) # Initial bias value b for the hidden node def sample_h(self, x): # Sample_h will activate hidden nodes for certain probabilty using Boltzmann distribution wx = torch.mm(x, self.W.t()) # Multiplying the two tensors x and W transposed. activation = wx + self.a.expand_as(wx) # Adding bias a p_h_given_v = torch.sigmoid(activation) # Using sigmoid to calculate probability whether to activate the hidden node or not. return p_h_given_v, torch.bernoulli(p_h_given_v) # Values of the hidden nodes are retuned in 2nd vector. Bernoulli function is used to set the values according to probability p_h (given v). def sample_v(self, y): wy = torch.mm(y, self.W) # Multiplying the two tensors y and W. activation = wy + self.b.expand_as(wy) # Adding bias b p_v_given_h = torch.sigmoid(activation) # Activation return p_v_given_h, torch.bernoulli(p_v_given_h) def train(self, v0, vk, ph0, phk): # Next, contrastive divergence will be performed. # v0 is the input vector for visbile nodes, vk is the result after k samplings, ph0 is the probability vector of the hidden, phk is the probability vector after k samplings self.W += (torch.mm(v0.t(), ph0) - torch.mm(vk.t(), phk)).t() # Updating the weight self.b += torch.sum((v0 - vk), 0) # Updating b, 0 is only added to make the size 2 self.a += torch.sum((ph0 - phk), 0) # Updating a nv = len(training_set[0])# Number of visible nodes nh = 100 # Define number of hidden nodes batch_size = 100 # Define batch size for training rbm = RBM(nv, nh)
# ### Training the RBM nb_epoch = 10 # Define number of complete passes through entire training data set for epoch in range(1, nb_epoch + 1): train_loss = 0 s = 0. for id_user in range(0, nb_users - batch_size, batch_size): # Training in batches. This training can also be done individually vk = training_set[id_user : id_user + batch_size] v0 = training_set[id_user : id_user + batch_size] ph0,_ = rbm.sample_h(v0) # Calculate initial probabilty to set hidden nodes for k in range(10): # Gibss sampling (markov chain monte carlo) for contrastive divergence. _,hk = rbm.sample_h(vk) # set the hidden node according to Bernoulli distribution _,vk = rbm.sample_v(hk) # set the visible node vk[v0<0] = v0[v0<0] # transfer -1 (unrated) from v0 to vk phk,_ = rbm.sample_h(vk) # Probability to set hidden node after k training steps. rbm.train(v0, vk, ph0, phk) # Update W, a and b train_loss += torch.mean(torch.abs(v0[v0 >= 0] - vk[v0 >= 0])) # calculate 'training loss' by taking the difference between the initial value and the subsequent values for ratings == 1. s += 1. print('epoch: '+str(epoch)+' loss: '+str(train_loss/s)) # Print normalised loss value
# ### Testing the RBM with a different dataset (test data set) test_loss = 0 s = 0. for id_user in range(nb_users): v = training_set[id_user:id_user+1] vt = test_set[id_user:id_user+1] # Save training_set and test_set of user 'id_user' as 2D array in v and vt if len(vt[vt>=0]) > 0: _,h = rbm.sample_h(v) # flip hidden neurons according to trained probability based on W and a _,v = rbm.sample_v(h) # flip visible neurons based on W and b test_loss += torch.mean(torch.abs(vt[vt>=0] - v[vt>=0]))# calculate the mean value of changes for visible neurons rated with 3 in test dataset s += 1. print('test loss: '+str(test_loss/s)) # print out normlized average change when using test data set instead of training set
Die eigentliche Stärke der RBM liegt aber darin generativ zu sein. Wir können uns für einen bestimmten Nutzer Filmvorschläge basierend auf seinen bisherigen Bewertungen machen lassen. In die Vorschläge gehen durch das Training des Netzwerkes natürlich auch die Bewertungen anderer Nutzer ein, die ähnliche Filme angeschaut haben.
# # Proposing new movies for a specific user based on his/her presvious ratings user_ID=67 # select user_ID # load dataset containing list of: movie id | movie title | release date | video release date | IMDb URL | unknown | Action | Adventure | Animation | Children's | Comedy | Crime | Documentary | Drama | Fantasy |Film-Noir | Horror | Musical | Mystery | Romance | Sci-Fi |Thriller | War | Western movie_set = pd.read_csv('/kaggle/input/mymod-dataset/u3.item', delimiter = '|') movie_set = np.array(movie_set) v = training_set[user_ID:user_ID+1] # select vector of user in training set v0=v # store original vector in v0 if len(v[v>=0]) > 0: _,h = rbm.sample_h(v) # flip h _,v = rbm.sample_v(h) # flip v v[v0<0] = v0[v0<0] # keep non rated or non liked moves as non raeted or non liked #print rated movies pos = (v0[0]== 1).nonzero(as_tuple=True) #select positions in training set rated w/ 3 stars movies = [movie_set[i][1] for i in pos[0]] #look up in position in movie_set print ("rated movies:") for movie in movies: print(movie) dv=v-v0 # calculate changes in rating #print proposals for new movies pos = (dv[0]== 1).nonzero(as_tuple=True) #select positions in training set rated w/ 3 stars movies = [movie_set[i][1] for i in pos[0]] #look up in position in movie_set print ("\n"+"new proposed movies:") for movie in movies: print(movie)
Keine Kommentare:
Kommentar veröffentlichen