Die Fourier-Transformation und die Unschärferelation in der Quantenmechanik

Die Fourier-Transformation hat vielerlei Anwendungen in der Mathematik, den  Ingenieurswissenschaften und in der Physik. Insbesondere in der Quantenmechanik vermittelt sie zwischen dem sogenannten Ortsraum eines Systems und dem Impulsraum. In ihren Eigenschaften kommt unter Anderem die Unschärfe zwischen Ort und Impuls eines quantenmechanischen Teilchens zum Ausdruck.

Beginnen möchte ich meine Überlegungen mit der zeitunabhängigen Schrödingergleichung.

$$\left(-\frac{\hbar^2}{2m}\Delta_r + V(\vec{r})\right)\psi (\vec{r}) = E \psi (\vec{r})$$

Dabei bezeichnet V(r) das Potential in dem sich das Teilchen bewegt, \(E\) die Energie des Systems, und \( \psi (\vec{r})\) die Wellenfunktion des Teilchens im Ortsraum. Des Weiteren bezeichnet \(\hbar\) das Wirkungsquantum, \(m\) die Masse des Teilchens, und \(\Delta_r = \nabla^2\) den sogenannten Laplaceoperator. Um den Zusammenhang zwischen Impuls p und Wellenlänge \(\lambda\) bzw.  Wellenzahl k zu verstehen, ist es hilfreich den einfachen Fall einer freien Bewegung, d.h. mit \( V(\vec{r}) = 0\), in einer Dimension zu betrachten. Die Schrödingergleichung vereinfacht sich zu

$$-\frac{\hbar^2}{2m}\left(\frac{\partial}{\partial x}\right)^2\psi=E\psi=\frac{1}{2}mv^2\psi=\frac{p^2}{2m}\psi .$$

Aus dieser Darstellung wird unmittelbar ersichtlich, dass der Operator für den Impuls sinnvollerweise als 

$$ \hat{p}:=\frac{\hbar}{i}\frac{\partial}{\partial x} \quad \mathsf{oder} \quad \hat{p}:=\frac{\hbar}{i}\nabla_r$$

definiert werden kann. Wenden wir den Operator z.B. auf eine gebundene Kreisbewegung in der komplexen Zahlenebene an, dann gilt

$$\begin{eqnarray}\hat{p}\, \psi (r)& = & \frac{\hbar}{i}\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y}\right)\left[\cos\left(\frac{2\pi}{\lambda}x\right)+i\sin\left(\frac{2\pi}{\lambda}x\right)\right] \\ & = &\frac{2\pi}{\lambda}\frac{\hbar}{i}\left[-\sin\left(\frac{2\pi}{\lambda}x\right)+i\cos\left(\frac{2\pi}{\lambda}x\right)\right] \\ & = & \frac{h}{\lambda} \, \psi(r),\end{eqnarray}$$

und daraus folgt \( p=\frac{h}{\lambda}=\hbar k \). Der Impuls hängt also über das Planksche Wirkungsquantum mit der Wellenlänge der Schwingung zusammen.

Allgemein lässt sich jede Wellenfunktion \(\psi\), die periodisch in \(k=2\pi / \lambda\) ist, als Fourierreihe schreiben. Dabei gilt \(n\lambda = 2\pi R\) mit \(n\) aus \( \mathbb{N}_0\) und \(R\) als  gedachtem Kreisradius auf dem sich die Schwingung ausbildet.

Die Fourierreihe lautet:

$$\begin{eqnarray} \psi(x) & = & \sum_{n = 0}^\infty A_n \cos \left( \frac{n}{R} x\right) + B_n \sin \left( \frac{n}{R}x \right) \\ & = & \sum_{n = -\infty}^\infty \psi_n e^{inx/R} \\ & = &\sum_{n = -\infty}^\infty \psi_n e^{ikx}\end{eqnarray}$$

Dabei haben wir uns der Eulerschen Formel \( e^{ikx} = \cos(kx) + i \sin(kx) \) bedient, und die Koeffizienten \(\psi_n\) als \(\psi_n =A_n + i B_n\) definiert. Um die Koeffizienten \(\psi_n\) zu bestimmen multiplizieren wir beide Seiten mit \(e^{-im x/R}\) . Dadurch ergibt sich:

$$e^{-i m x/R}\psi(x) = \sum_{n = -\infty}^\infty \psi_n e^{i(n-m)x/R}$$

Als Nächstes  integrieren wir beide Seiten dieser Gleichung über den Umfang eines Kreises.

$$\int\limits_{-\pi R}^{\pi R} \mathrm{d}x~e^{-i m x/R}\psi(x) = \sum_{n = -\infty}^\infty \psi_n \int\limits_{-\pi R}^{\pi R} \mathrm{d}x~ e^{i(n-m)x/R}$$

Der kompliziert erscheinende Ausdruck lässt sich deutlich vereinfachen, denn es gilt

$$\int\limits_{-\pi R}^{\pi R} \mathrm{d}x~ e^{i(n-m)x/R}=\begin{cases}\displaystyle 2\pi R \quad ;n = m\\ \displaystyle 0 \qquad \ ;n\neq m\end{cases}$$

und daraus folgt

$$\int\limits_{-\pi R}^{\pi R} \mathrm{d}x~e^{-i m x/R}\psi(x)  = 2\pi R \psi_m.$$

Die Koeffizienten \(\psi_m\) ergeben sich nach Umstellen zu

$$\psi_n = \frac{1}{2\pi R}\int\limits_{-\pi R}^{\pi R} \mathrm{d}x~e^{-i n x/R}\psi(x)\quad (*)$$

Für \(R\rightarrow\infty\) lässt sich dieser Zusammenhang auf nicht periodische \(\psi(x)\) verallgemeinern. Zunächst führen wir \(\Delta k=\frac{1}{R}\) und eine 'Dichtefunktion' \(\hat{\psi}(k) = \sqrt{2\pi}R\psi_n\) ein. Dann gilt

$$\begin{eqnarray}\psi(x) & = & \sum_{n=-\infty}^\infty \psi_n e^{ikx}\\ & = &\sum_{k=n / R} \Delta k \cdot \frac{1}{\sqrt{2\pi}}\hat{\psi}(k)e^{ikx}\end{eqnarray}$$

und im Grenzfall \(R\rightarrow\infty\) ergibt sich

$$\psi(x) = \frac{1}{\sqrt{2\pi}} \int\limits_{-\infty}^\infty\mathrm{d}k~ e^{ikx} \hat{\psi}(k) \quad (1)$$

Die 'Koeffizientenfunktion' \(\hat{\psi}(k)\) ergibt sich unter Zuhilfenahme von (*) im Grenzfall  \(R\rightarrow\infty\) zu

$$\begin{eqnarray}\hat{\psi}(k) & = & \sqrt{2\pi}R \; \psi_n \\ & = & \sqrt{2\pi}R\frac{1}{2\pi R}\int\limits_{-\infty}^\infty \mathrm{d}x~ e^{-ikx}\psi(x)\ \\ & = & \frac{1}{\sqrt{2\pi}}\int\limits_{-\infty}^\infty \mathrm{d}x~ e^{-ikx}\psi(x) \quad (2) \end{eqnarray}$$ 

Die Gleichungen (1) und (2) bilden die weithin bekannte Fouriertransformation. Durch die Symmetrie der Gleichungen wird die Äquivalenz der Darstellung einer Wellenfunktion \(\psi (x)\) im Ortsraum und der Darstellung \(\psi (k)\) im Impulsraum deutlich. 

Inwiefern darin auch die Unschärfebeziehung zwischen Impuls und Ort zum Ausdruck kommt, möchte ich anhand eines Beispiels zeigen. Die Wellenfunktion \(\psi(x)\) eines Teilchens sei wie folgt von -a bis +a um einen Nullpunkt lokalisiert.

Da in der Quantenmechanik die Aufenthaltswahrscheinlichkeit eines Teilchens durch \(\psi^2\) gegeben ist, soll die Amplitude der Wellenfunktion \(1/\sqrt{2a}\) betragen. Dies gewährleistet, dass das Quadrat der Wellenfunktion eine Fläche von 1 zwischen  -a und +a einschließt.

Setzt man \(\psi(x)\) in Gleichung (1) ein, dann ergibt sich:

$$\hat{\psi}(k) = \frac{1}{\sqrt{2\pi}} \frac{1}{\sqrt{2a}}\int\limits_{-a}^a \mathrm{d}x~e^{-ikx} = \frac{1}{\sqrt{\pi a}} \frac{1}{-ik}(e^{-ika} - e^{ika} ) =  \frac{1}{\sqrt{\pi a} }\frac{\sin (ka)}{k}$$

Grafisch lässt sich das als gedämpfte Schwingung mit einem Maximum am Ort 0 darstellen.

Lokalisieren wir das Teilchen im Ortsraum weniger stark und vergrößern a, dann verkleinert sich die Periode der Schwingung, und es bildet sich im k-Raum ein starker Peak um 0 aus. Ein sehr kleines Intervall von k Werten kann also mit hoher Wahrscheinlichkeit beobachtet werden.

Wenn wir das Teilchen im Ortsraum sehr stark lokalisieren und a sehr klein machen, wird \(\psi(k)\) weitgehend unabhängig von k. Für die Sinusfunktion gilt die sogenannte  Kleinwinkelnäherung. Es gilt:

$$\hat{\psi}(k)=\frac{1}{\sqrt{\pi a}}\frac{ka}{k}=\sqrt{a}{\pi}$$

Die Wellenfunktion ist über den gesamten k-Raum verschmiert. Es lässt sich kein einzelner k-Wert finden, der sich durch ein großes \(\psi(k)\) auszeichnet. Der Impuls ist unbestimmbar.

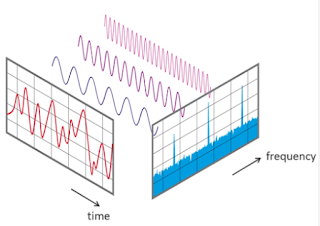
Der Vollständigkeit halber sei zum Abschluss noch erwähnt, dass das Prinzip der Unschärfe natürlich für alle physikalischen Größen und deren Fouriertransformierte gilt. Die Unschärfebeziehung ist also keine Eigenschaft der Quantenmechanik sondern findet sich auch in anderen Bereichen wie z.B der Signalverarbeitung wieder. Bedingt durch die Unschärfebeziehung ist es z.B. nicht möglich das genaue Frequenzspektrum eines Signals zu einem bestimmten Zeitpunkt zu messen.

Die Formeln in diesem Beitrag wurden übrigens mit MathJax erstellt. Es genügt ein kleines 'Code-Snippet' als 'Gadget' ins Layout des blogs einzufügen, und schon werden die TeX Befehle, die man in den Editor schreibt, in der Webansicht wohl gesetzt dargestellt.

Viel Spaß beim selber rechnen, schreiben und nachdenken...